Diese Seite funktioniert nur mit Javascript.
Angebotsfunktion einer Unternehmung3.5.1.1 Kurz- und langfristige AngebotsfunktionFaktornachfrage
lle Überlegungen, die bisher zur Angebotsfunktion angestellt wurden, waren unabhängig von der Fristigkeit der Betrachtung. Aus einer kurzfristigen Kostenfunktion lässt sich über die Regel "Preis gleich Grenzkosten" die Angebotsfunktion für eine Unternehmung ebenso ermitteln wie aus einer langfristigen. Kurzfristig hat die Unternehmung aber nicht die Möglichkeit, alle Produktionsfaktoren optimal anzupassen. Das lässt folgende Plausibilitätsüberlegung zu: In Abbildung 1 sei zum Preis p* die Menge x* das langfristig optimale Angebot, bei dem die Unternehmung beide Produktionsfaktoren, Arbeit und Kapital, optimal einsetzt. Kurzfristig kann die Produktion nur an veränderte Preise angepasst werden, indem der (als kurzfristig variabel angenommene) Arbeitseinsatz variiert wird. Eine Ausdehnung der Produktion bei steigendem Marktpreis würde dann höhere Grenzkosten verursachen (blau) als langfristig in Kauf zu nehmen wären. Denn auf lange Sicht könnte ja auch der Kapitaleinsatz wieder optimal gestaltet werden (rot), d. h. die Unternehmung wieder die kostenminimale Kapitalintensität wählen.
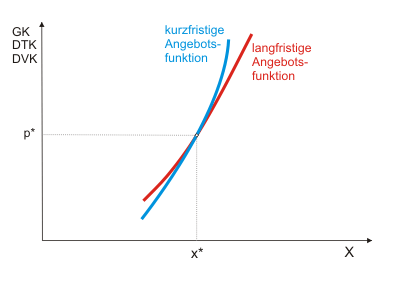
Umgekehrt wäre im Fall eines rückläufigen Marktpreises zu beobachten, dass die Unternehmung ihr Angebot einschränken wollte. Zwar kann sie sofort mit einer Reduktion des Arbeitseinsatzes (zu deutsch: Entlassungen) reagieren, der Kapitaleinsatz ist dann aber kurzfristig überoptimal. Das bedeutet, die Kosten gehen mit der Produktionsminderung kurzfristig nicht so stark zurück wie langfristig. Somit liegt die kurzfristige Grenzkostenkurve unter der langfristigen. Das bedeutet, dass kurzfristige Anpassungen der Unternehmung an Preise weniger elastisch erfolgen als langfristige.
Nun, dieser Zusammenhang ist etwas schwierig. Vielleicht kann ihn das folgende Beispiel verdeutlichen: Angenommen, eine Unternehmung produziert mit der linear homogenen Produktionsfunktion $ x = L^{0,5}K^{0,5}$ vom Cobb-Douglas-Typ. Die konstanten Skalenerträge führen dann zu langfristig konstanten Stückkosten. Liegt der Preis genau auf der Höhe der langfristigen Stückkosten, ist das Angebot unbestimmt, denn jede Produktionsmenge führt zu einem Gewinn in Höhe von null. Auf Preisänderungen würde das Unternehmen langfristig sehr sensitiv reagieren, denn die langfristige Grenzkostenkurve verläuft bei konstanten Stückkosten waagerecht. Kurzfristig kann aber nur der Faktor Arbeit angepasst werden. Die Erträge unterliegen in der kurzen Frist dem Gesetz vom abnehmenden Ertragszuwachs, so dass steigende Grenzkosten vorliegen. Also besitzt die Angebotsfunktion kurzfristig eine positive Steigung. Während die langfristige Angebotsfunktion in diesem Beispiel also unendlich elastisch ist, besitzt die kurzfristige Angebotsfunktion eine endliche Elastizität.
Auf lange Sicht kommt noch ein weiterer wichtiger Faktor hinzu. Langfristig können Unternehmen in den Markt eintreten oder ausscheiden. Darauf geht der übernächste Abschnitt ein.